Mayo–Lewis equation
The Mayo-Lewis equation or copolymer equation in polymer chemistry describes the distribution of monomers in a copolymer [1]:
Taking into consideration a monomer mix of two components 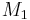 and
and 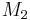 and the four different reactions that can take place at the reactive chain end terminating in either monomer (
and the four different reactions that can take place at the reactive chain end terminating in either monomer (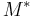 ) with their reaction rate constants
) with their reaction rate constants 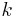 :
:
and with reactivity ratios defined as:
the copolymer equation is given as:
with the concentration of the components given in square brackets. The equation gives the copolymer composition at any instant during the polymerization.
Contents |
Limiting cases
From this equation several limiting cases can be derived:
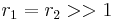 with both reactivity ratios very high the two monomers have no inclination to react to each other except with themselves leading to a mixture of two homopolymers.
with both reactivity ratios very high the two monomers have no inclination to react to each other except with themselves leading to a mixture of two homopolymers.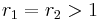 with both ratios larger than 1, homopolymerization of component M_1 is favored but in the event of a crosspolymerization by M_2 the chain-end will continue as such giving rise to block copolymer
with both ratios larger than 1, homopolymerization of component M_1 is favored but in the event of a crosspolymerization by M_2 the chain-end will continue as such giving rise to block copolymer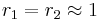 with both ratios around 1, monomer 1 will react as fast with another monomer 1 or monomer 2 and a random copolymer results.
with both ratios around 1, monomer 1 will react as fast with another monomer 1 or monomer 2 and a random copolymer results.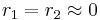 with both values approaching 0 the monomers are unable to react in homopolymerization and the result is an alternating polymer
with both values approaching 0 the monomers are unable to react in homopolymerization and the result is an alternating polymer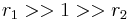 In the initial stage of the copolymerization monomer 1 is incorporated faster and the copolymer is rich in monomer 1. When this monomer gets depleted, more monomer 2 segments are added. This is called composition drift.
In the initial stage of the copolymerization monomer 1 is incorporated faster and the copolymer is rich in monomer 1. When this monomer gets depleted, more monomer 2 segments are added. This is called composition drift.
An example is maleic anhydride and stilbene, with reactivity ratio:
- Maleic anhydride (
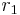 = 0.08) & cis-stilbene (
= 0.08) & cis-stilbene (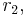 = 0.07)
= 0.07) - Maleic anhydride (
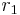 = 0.03) & trans-stilbene (
= 0.03) & trans-stilbene (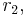 = 0.03)
= 0.03)
Both of these compounds do not homopolymerize and instead, they react together to give exclusively alternating copolymer.
Another form of the equation is:
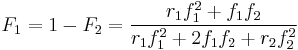
where 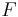 stands the mole fraction of each monomer in the copolymer:
stands the mole fraction of each monomer in the copolymer:
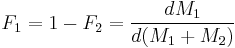
and 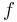 the mole fraction of each monomer in the feed:
the mole fraction of each monomer in the feed:
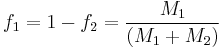
When the copolymer composition has the same composition as the feed, this composition is called the azeotrope.
Calculation of reactivity ratios
The reactivity ratios can be obtained by rewriting the copolymer equation to:
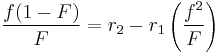
with
![f = \frac{[M_1]}{[M_2]} \,](/2012-wikipedia_en_all_nopic_01_2012/I/57ac5143d99e53b5e8306a154f6cd38c.png) in the feed
in the feed
and
![F = \frac{d[M_1]}{d[M_2]} \,](/2012-wikipedia_en_all_nopic_01_2012/I/bbc930eec4a70fde6beec25cd2ee4320.png) in the copolymer
in the copolymer
A number of copolymerization experiments are conducted with varying monomer ratios and the copolymer composition is analysed at low conversion. A plot of 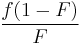 versus
versus 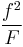 gives a straight line with slope
gives a straight line with slope 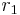 and intercept
and intercept 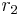 .
.
A semi-empirical method for the determination of reactivity ratios is called the Q-e scheme.
Equation derivation
Monomer 1 is consumed with reaction rate [2]:
![\frac{-d[M_1]}{dt} = k_{11}[M_1]\sum[M_1^*] %2B k_{21}[M_1]\sum[M_2^*] \,](/2012-wikipedia_en_all_nopic_01_2012/I/3dc78c19a18377553151beae43a910e4.png)
with ![\sum[M_x^*]](/2012-wikipedia_en_all_nopic_01_2012/I/bbd242d963a5c6db2d1c721018379467.png) the concentration of all the active centers terminating in monomer 1 or 2.
the concentration of all the active centers terminating in monomer 1 or 2.
Likewise the rate of disappearance for monomer 2 is:
![\frac{-d[M_2]}{dt} = k_{12}[M_2]\sum[M_2^*] %2B k_{22}[M_2]\sum[M_1^*] \,](/2012-wikipedia_en_all_nopic_01_2012/I/11a8f22254486279b3cd3fe2ae132584.png)
Division of both equations yields:
![\frac{d[M_1]}{d[M_2]} = \frac{[M_1]}{[M_2]} \left( \frac{k_{11}\frac{\sum[M_1^*]}{\sum[M_2^*]} %2B k_{21}} {k_{12}\frac{\sum[M_1^*]}{\sum[M_2^*]} %2B k_{22}} \right) \,](/2012-wikipedia_en_all_nopic_01_2012/I/72052d769109adc65bfc1f22188ebbe3.png)
The ratio of active center concentrations can be found assuming steady state with:
![\frac{d\sum[M_1^*]}{dt} = \frac{d\sum[M_2^*]}{dt} \approx 0\,](/2012-wikipedia_en_all_nopic_01_2012/I/a0d91130d633c58b23337bfd2ca3b8cb.png)
meaning that the concentration of active centres remains constant, the rate of formation for active center of monomer 1 is equal to the rate of their destruction or:
![k_{21}[M_1]\sum[M_2^*] = k_{12}[M_2]\sum[M_1^*] \,](/2012-wikipedia_en_all_nopic_01_2012/I/166df310517c5eacaedeb43162a032f2.png)
or
![\frac{\sum[M_1^*]}{\sum[M_2^*]} = \frac{k_{21}[M_1]}{k_{12}[M_2]}\,](/2012-wikipedia_en_all_nopic_01_2012/I/9dc9c686459d79d062be7dcd0a3d339b.png)
External links
References
- ^ Copolymerization. I. A Basis for Comparing the Behavior of Monomers in Copolymerization; The Copolymerization of Styrene and Methyl Methacrylate Frank R. Mayo and Frederick M. Lewis J. Am. Chem. Soc.; 1944; 66(9) pp 1594 - 1601; doi:10.1021/ja01237a052
- ^ Introduction to polymers R.J. Young ISBN 0412221705
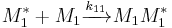
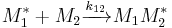
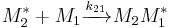
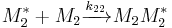
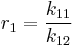
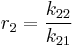
![\frac {d\left [M_1 \right]}{d\left [M_2\right]}=\frac{\left [M_1\right]\left (r_1\left[M_1\right]%2B\left [M_2\right]\right)}{\left [M_2\right]\left (\left [M_1\right]%2Br_2\left [M_2\right]\right)}](/2012-wikipedia_en_all_nopic_01_2012/I/dea8c560dd0363f25dc92f414a5b64f6.png)